A lógica paraconsistente
25
set
O paradoxo de Kurt Gödel, que um sistema completo é inconsistente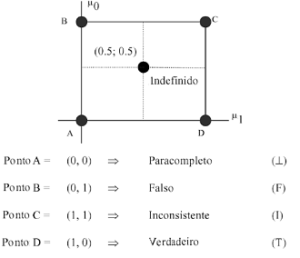
foi fundamental para uma nova fase nos princípios lógico formais, e cooperou com o surgimento do computador.
Foi o filósofo peruano Francisco Miró Quesada, desconhecido de muitos estudiosos da América Latina, que cunhou a palavra paraconsistente em 1976.
O brasileiro Newton da Costa que desenvolveu esta teoria que tornou-se muito importante para diversas áreas, entre elas a filosofia e a Inteligência Artificial.
Na figura ao lado o eixo que vai de u 0 a u 1 é chamado de grau de crença, mas a verdade tem os pontos A para consistente e C para inconsistente, tendo muita aplicação ao cotidiano.
O estudo aplicado a semântica, explora principalmente os paradoxos, por exemplo, pode-se afirmar que um homem cego, enxerga sobre certas circunstâncias, também o estudo de diversas formas de percepção e habilidades poderá ajudar os parâmetros da deep mind.
Já afirmamos, que justamente o neologicismo poderá ajudar a IA nesta fase de deep intelligence, por exemplo, no estudo das linguagens naturais, a linguagem do dia-a-dia.
A ideia que possa existir A e não-A era inconcebível na filosofia ocidental, é o princípio do terceiro excluído, que vem de Parménides e foi consolidado em Aristóteles.
As lógicas paraconsistentes são propositalmente mais “fracas”, termos para se referir a esta ruptura com a lógica clássica, pois elas resolvem poucas inferências proposicionais válidas no sentido clássico da lógica
A lógica das linguagens paraconsistentes no entanto são mais conservadoras que as de contrapartidas clássicas, e isto muda hierarquia da metalinguagem feita por Alfred Tarski.
A influencia na linguagem natural foi antecipada em 1984 por Solomon Feferman que afirmou “…a linguagem natural abunda em expressões direta ou indiretamente autorreferenciais, embora aparentemente inofensivas, todas as quais são excluídas do arcabouço tarskiano”, isto porque no cotidiano, em verdade somos paraconsistentes.
